177
о. Четвертые и другие законы структуры и ее симметрии
Постоянную интегрирования, как и в случае уравнения (92), принимаем равной нулю.
I Для термической степени свободы это уравнение приводит
к соотношению
к соотношению
1 Дифференциальное соотношение (тождество) термодинамики, выражающее пятый закон симметрии структуры первого порядка, находится прежним способом — путем дифференцирования равенств (208) по Ει и Рь В окончательном виде имеем
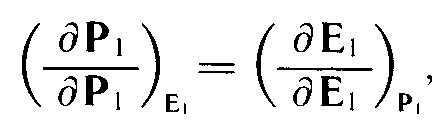 (212)
(212)
или
_____ 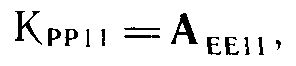 (213)
(213)
где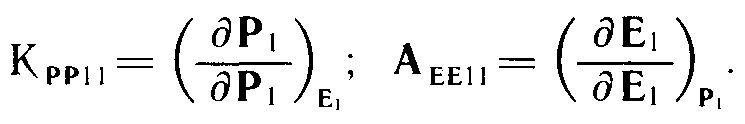
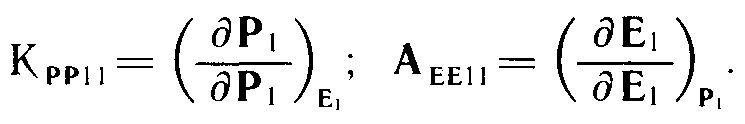
В этих равенствах приращения интенсиала и экстенсора не сокращаются, так как относятся к совершенно различным условиям взаимодействия (сопряжения) системы и окружающей среды.
Пятая характеристическая функция, подобно третьей, имеет своего двойника. Он получается, если воспользоваться шестым аргументом набора (160). Это равносильно тому, что во всех равенствах пятой функции индекс 1 заменяется на индекс 2. Шестая характеристическая функция имеет вид
Для механической степени свободы термомеханической системы последнее уравнение дает вторую составляющую энергии 1/2- Имеем
Очевидно, что суммарная энергия U для системы с двумя степенями свободы должна быть равна сумме первого U\ и второго L/2 компонентов энергии, то есть
Для термомеханической системы в целом